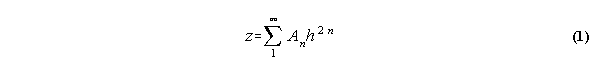
I started out looking at this while puzzling over the problem of how to turn my polished f/3.9 mirror into a paraboloid, which by a naive calculation was going to require something like 6 waves of total correction (at the surface) to make. Taking off from comments of Jim Burrows I ended up working on the problem of solving for the paraboloid having minimum area weighted rms deviations from a given curve. As a preliminary comment, I'm working at the surface of the glass here. The same analysis works for the wavefront evaluated at the center of curvature or focus, modulo factors of 2 or so (which in my universe don't count anyway).

Notation

I more or less follow the notational conventions of Rutten & van Venrooij (1988; R&vV) here: the optical surface is taken as tangent to the x-y plane, with the z axis corresponding to the optical axis. The origin is at the optical center. Radial distance in the x-y plane is denoted by h.

The mirror's paraxial radius of curvature is r, and it's physical radius is R.

Model and solution

The simple way to approach this is to represent our existin>Model and solution

The simple way to approach this is to represent our existing curve with a generic power series in h,

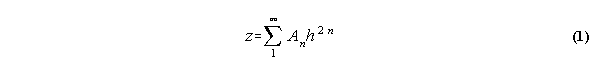
Our target paraboloid has equation z_t = h²/(2r_t). I'm imagining working actual glass here, so I allow a change of origin c between the existing curve and the target paraboloid. The area weighted integrated square difference between the existing and target curve is (ignoring a factor 2pi):

 

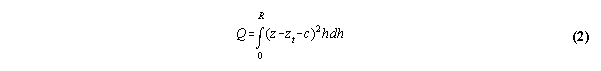
and the weighted mean square error is

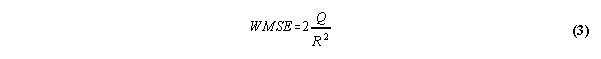
We want to minimize Q (or equivalently WMSE) with respect to the free parameters r_t and c. I'll briefly outline how to do this -- it's pretty straightforward, but tedious. The first order necessary conditions (which I think are also sufficient for this case) for a minimum are:

The rest is just paperwork. Here's the solutions:

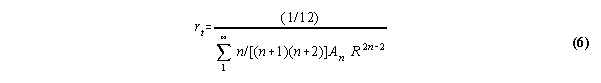
The rest is just paperwork. Here's the solutions:

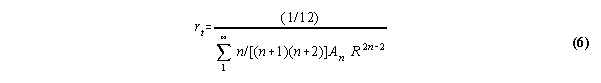
and
 
 

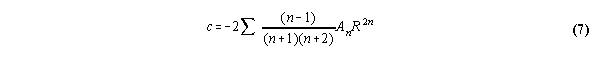
Substituting equations 6 and 7 into 2 and 3 we get, with more tedious algebra:
 
 

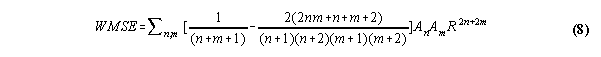
I don't see a correspondingly simple way to get P-V. The equation of the surface deviation is of course a power series in h, which in general could have many local extrema. Except in special cases one would have to evaluate all of them to calculate P-V -- not a simple task. One special case that is easy though is the 2^nd order approximation (ie terms in h^2 and h^4).

2^nd order approximation

Solutions:

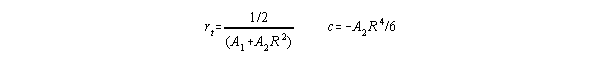
and

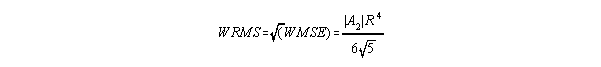
Substituting the solution for r_t back in the expression for surface deviation we get (we don't need c)

&_t back in the expression for surface deviation we get (we don't need c)

Now this has local extrema at h=0, R/sqrt(2), and R, and therefore

and

independent of the shape of the curve, implying among other things that at this level of approximation statements about "P-V" errors are equivalent to statements about WRMS errors (apart from a constant factor). This confirms analytically what I speculated based on plugging numbers into a spreadsheet. The ratio I get differs by a few percent from the value given by Born & Wolf of 2 sqrt(3). Perhaps they based their analysis on unweighted RMS errors. Of course a mistake on my part can't be ruled out.

For a conic section, a binomial expansion gives A₂ = (1+b)/(8r³). Substituting D=2R and f=r/2 we can find a criterion for acceptable defective surfaces:

The value of k corresponding to Rayleigh's criterion (1/8 wave at the surface) is 12 sqrt(5), so rearranging we get

  so rearranging we get

or at 550 nm,

which is within a fraction of a percent of the value given in Texereau (I think he adopts a default wavelength of 560nm, which would account for the small difference.

Comments

All of this analysis assumes the target is a paraboloid of freely adjustable focal length. For surfaces of interest to the ATM the difference in r between a given curve and it's best fitting target paraboloid will usually be measured in fractions of a millimeter -- for most ATM projects this is of no consequence. The same assumption is implicit in Texereau's foucault data reduction procedures. Of course if we're truly aiming at a fixed target the analysis will be different.

I haven't looked at the case where the target is a surface other than paraboloid. My guess is that the analysis would be much messier, but the mathematics here isn't particularly deep.

I haven't looked in any detail at cases where higher order terms in the power series for the existing curve are significant. I anticipate though that the constant relation between P-V and WRMS breaks down for realistic curves. For example the broad defects that I'm getting right now on my f/4 mirror result in estimated P-V/WRMS ~ 2 (I'm usingdefects that I'm getting right now on my f/4 mirror result in estimated P-V/WRMS ~ 2 (I'm using a 3^rd order estimate of the existing curve from foucault test data). Conversely a few large mirrors for professional observatories that I've happened across on the web have reported P-V/RMS ~ 10 or more. In the latter case I suspect what's happening is that the use of local polishers is resulting in lots of low amplitude, small scale errors, with a few much larger departures thrown in.

Michael Peck
10 Sep 97
mailto:mpeck1@ix.netcom.com
 
  nbsp;